The realm of quantum computing is consistently making strides, particularly in the field of superconducting quantum simulators. Recent collaborative research efforts involving the Freie Universität Berlin, University of Maryland and NIST, Google AI, and Abu Dhabi have focused on efficiently determining the parameters of free Hamiltonians governing bosonic excitations. Their work not only addresses key challenges but also paves the way for breakthroughs that could outstrip classical computing capabilities. This article delves into their methodologies, the challenges they faced, and the broader implications of their findings.
Jens Eisert, the lead author of the study, had an intriguing epiphany during a conference while addressing a call for assistance from colleagues involved in calibrating Google AI’s Sycamore superconducting quantum chip. Initially, he perceived the task of identifying Hamiltonians—a mathematical construct fundamental to quantum mechanics—as straightforward. However, as discussions evolved, it became obvious that accurately recovering Hamiltonian parameters was fraught with complications. The intricacies of measuring frequencies and employing Hamiltonian learning methods raised considerable hurdles.
Eisert’s resolve did not falter; he reached out to gifted Ph.D. students, including Ingo Roth and Dominik Hangleiter, encouraging collaborative brainstorming to find a solution. Over the years, their research continually evolved, and along the way, another bright mind, Jonas Fuksa, joined the quest. The collective expertise gradually transformed theoretical frameworks into robust practical applications, culminating in profound insights into Hamiltonian learning’s real-world implications.
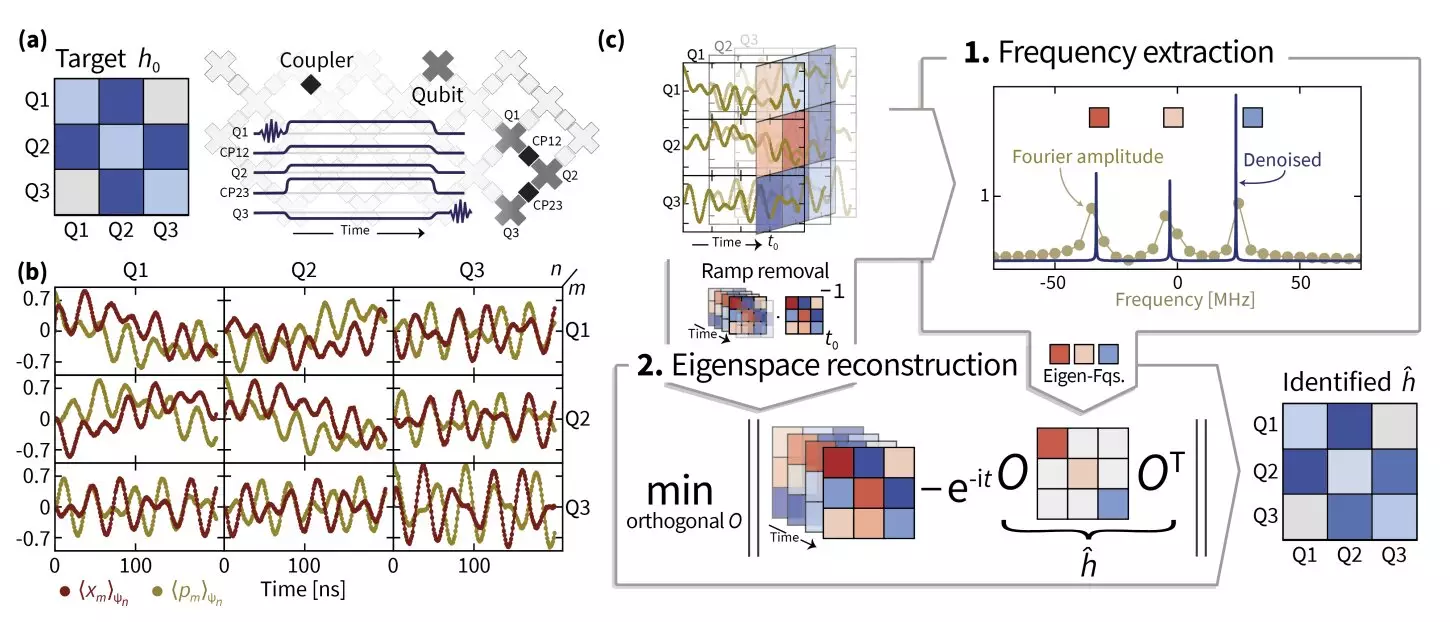
The interdisciplinary team employed novel methodologies to tackle the reconstruction of Hamiltonian dynamics effectively. Their pioneering use of superresolution techniques enhanced the resolution of eigenvalue estimations. This critical step allowed the researchers to elucidate the Hamiltonian frequencies accurately, a feat essential to the identification of the Hamiltonian operator involved in superconducting quantum simulations.
Complementing superresolution, the researchers utilized manifold optimization techniques. This method improves upon traditional optimization for complex variables existing on curved spaces rather than flat Euclidean terrains. Eisert highlighted that understanding Hamiltonian switching processes proved vital. The inherent imperfections in the process, characterized by non-instantaneous and non-unitary transitions, posed significant challenges. Therefore, it became crucial to account for these discrepancies to avert inaccuracies in Hamiltonian evolution fits.
The culmination of this research led to the advent of a novel technique dubbed TensorEsprit, designed to enhance signal processing approaches. By amalgamating TensorEsprit with manifold optimization, the researchers successfully identified Hamiltonian parameters in superconducting qubits—specifically, up to 14 coupled qubits across two Sycamore processors. This achievement showcased not just the robustness of their methods but also underscored the potential scalability when applied to extensive quantum computing systems.
Despite these advancements, the authors candidly acknowledged the few publications in the domain of Hamiltonian learning—a reflection of the inherent complexities of translating theoretical models into practical methodologies. Their work signals a monumental step towards rectifying this gap, offering insight into why tangible data and findings have been scarce.
The Future of Quantum Simulations
The implications of these findings extend into the future of quantum technology development. As the team plans to adapt their strategies to further explore interacting quantum systems, they also seek to apply their frameworks to quantum systems composed of cold atoms. With roots extending back to the pivotal studies of physicist Immanuel Bloch, this research could potentially open avenues for investigation into quantum phenomena previously thought to be opaque.
Eisert emphasized that understanding a system’s Hamiltonian is foundational yet often overlooked in the discourse surrounding quantum mechanics. The dependency on experimental data necessitates precise knowledge of Hamiltonian operators to garner predictive understanding. Thus, dissecting the methods to learn Hamiltonians from empirical data aligns with broader ambitions in quantum simulations.
The synergy between theoretical formulation and empirical validation marks the ongoing journey of quantum simulation research. With their innovative methodologies, Eisert and his colleagues not only elucidate complex Hamiltonian identifications but also set the stage for future exploration in quantum technology. Their findings resonate with the core tenets of modern physics—demonstrating an unwavering pursuit to bridge the gap between abstract theory and practical outcomes in quantum computing. As research continues, it is anticipated that their contributions will fuel significant advancements in analog quantum simulation, unlocking possibilities within this cutting-edge field.